A 4-cusped Hypocycloid which is sometimes also called a Tetracuspid, Cubocycloid, or Paracycle.
The parametric equations of the astroid can be obtained by plugging in  or
or  into the equations for a
general Hypocycloid, giving
into the equations for a
general Hypocycloid, giving
In Cartesian Coordinates,
 |
(3) |
In Pedal Coordinates with the Pedal Point at the center, the equation is
 |
(4) |
The Arc Length, Curvature, and Tangential Angle are
As usual, care must be taken in the evaluation of  for
for  . Since (5) comes from an integral involving the
Absolute Value of a function, it must be monotonic increasing. Each Quadrant can be treated correctly by
defining
. Since (5) comes from an integral involving the
Absolute Value of a function, it must be monotonic increasing. Each Quadrant can be treated correctly by
defining
 |
(8) |
where
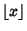 is the Floor Function, giving the formula
is the Floor Function, giving the formula
![\begin{displaymath}
s(t)=(-1)^{1+[n{\rm\ (mod\ 2)}]} {\textstyle{3\over 2}}\sin^2 t+3\left\lfloor{{\textstyle{1\over 2}}n}\right\rfloor .
\end{displaymath}](a_1820.gif) |
(9) |
The overall Arc Length of the astroid can be computed from the general Hypocycloid formula
 |
(10) |
with  ,
,
 |
(11) |
The Area is given by
 |
(12) |
with  ,
,
 |
(13) |
The Evolute of an Ellipse is a stretched Hypocycloid. The gradient of the Tangent  from
the point with parameter
from
the point with parameter  is
is  . The equation of this Tangent
. The equation of this Tangent  is
is
 |
(14) |
(MacTutor Archive).
Let  cut the x-Axis and the y-Axis at
cut the x-Axis and the y-Axis at  and
and  , respectively. Then the length
, respectively. Then the length  is a constant
and is equal to
is a constant
and is equal to  .
.
The astroid can also be formed as the Envelope produced when a Line Segment is moved with each end on one of a
pair of Perpendicular axes (e.g., it is the curve enveloped by a ladder sliding against a wall or a garage door with the
top corner moving along a vertical track; left figure above). The astroid is therefore a Glissette. To see this, note
that for a ladder of length  , the points of contact with the wall and floor are
, the points of contact with the wall and floor are  and
and
 ,
respectively. The equation of the Line made by the ladder with its foot at
,
respectively. The equation of the Line made by the ladder with its foot at  is therefore
is therefore
 |
(15) |
which can be written
 |
(16) |
The equation of the Envelope is given by the simultaneous solution of
 |
(17) |
which is
Noting that
allows this to be written implicitly as
 |
(22) |
the equation of the astroid, as promised.
The related problem obtained by having the ``garage door'' of length  with an ``extension'' of length
with an ``extension'' of length  move up and down a slotted track also gives a surprising answer. In this case, the position of the ``extended''
end for the foot of the door at horizontal position
move up and down a slotted track also gives a surprising answer. In this case, the position of the ``extended''
end for the foot of the door at horizontal position  and Angle
and Angle  is given by
is given by
Using
 |
(25) |
then gives
Solving (26) for  , plugging into (27) and squaring then gives
, plugging into (27) and squaring then gives
 |
(28) |
Rearranging produces the equation
 |
(29) |
the equation of a (Quadrant of an) Ellipse with Semimajor and Semiminor Axes of lengths  and
and  .
.
The astroid is also the Envelope of the family of Ellipses
 |
(30) |
illustrated above.
See also Deltoid, Ellipse Envelope, Lamé Curve, Nephroid, Ranunculoid
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 172-175, 1972.
Lee, X. ``Astroid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Astroid_dir/astroid.html.
Lockwood, E. H. ``The Astroid.'' Ch. 6 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 52-61, 1967.
MacTutor History of Mathematics Archive. ``Astroid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Astroid.html.
Yates, R. C. ``Astroid.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 1-3, 1952.
© 1996-9 Eric W. Weisstein
1999-05-25

![]() or
or ![]() into the equations for a
general Hypocycloid, giving
into the equations for a
general Hypocycloid, giving


![]() , the points of contact with the wall and floor are
, the points of contact with the wall and floor are ![]() and
and
![]() ,
respectively. The equation of the Line made by the ladder with its foot at
,
respectively. The equation of the Line made by the ladder with its foot at ![]() is therefore
is therefore




![]() with an ``extension'' of length
with an ``extension'' of length ![]() move up and down a slotted track also gives a surprising answer. In this case, the position of the ``extended''
end for the foot of the door at horizontal position
move up and down a slotted track also gives a surprising answer. In this case, the position of the ``extended''
end for the foot of the door at horizontal position ![]() and Angle
and Angle ![]() is given by
is given by


