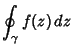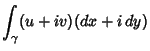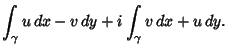If 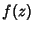 is analytic and its partial derivatives are continuous throughout some simply connected region
is analytic and its partial derivatives are continuous throughout some simply connected region 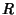 , then
, then
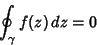 |
(1) |
for any closed Contour 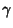 completely contained in
completely contained in 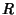 . Writing
. Writing  as
as
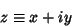 |
(2) |
and 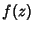 as
as
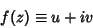 |
(3) |
then gives
From Green's Theorem,
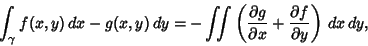 |
(5) |
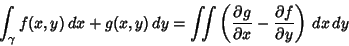 |
(6) |
so (4) becomes
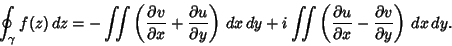 |
(7) |
But the Cauchy-Riemann Equations require that
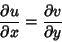 |
(8) |
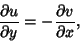 |
(9) |
so
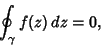 |
(10) |
Q. E. D.
For a Multiply Connected region,
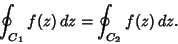 |
(11) |
See also Cauchy Integral Theorem, Morera's Theorem, Residue Theorem (Complex Analysis)
References
Arfken, G. ``Cauchy's Integral Theorem.'' §6.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL:
Academic Press, pp. 365-371, 1985.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill,
pp. 363-367, 1953.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is analytic and its partial derivatives are continuous throughout some simply connected region
is analytic and its partial derivatives are continuous throughout some simply connected region ![]() , then
, then