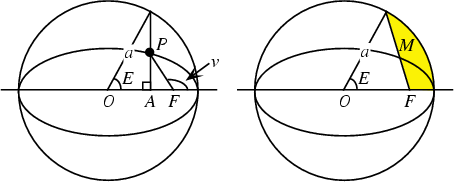
The Angle obtained by drawing the Auxiliary Circle of an Ellipse with center 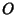 and Focus
and Focus 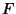 , and
drawing a Line Perpendicular to the Semimajor Axis and intersecting it at
, and
drawing a Line Perpendicular to the Semimajor Axis and intersecting it at 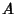 . The Angle
. The Angle  is
then defined as illustrated above. Then for an Ellipse with Eccentricity
is
then defined as illustrated above. Then for an Ellipse with Eccentricity 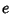 ,
,
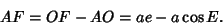 |
(1) |
But the distance 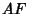 is also given in terms of the distance from the Focus
is also given in terms of the distance from the Focus 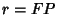 and the
Supplement of the Angle from the Semimajor Axis
and the
Supplement of the Angle from the Semimajor Axis 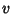 by
by
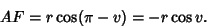 |
(2) |
Equating these two expressions gives
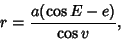 |
(3) |
which can be solved for 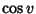 to obtain
to obtain
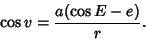 |
(4) |
To get  in terms of
in terms of 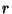 , plug (4) into the equation of the Ellipse
, plug (4) into the equation of the Ellipse
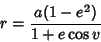 |
(5) |
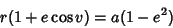 |
(6) |
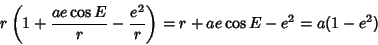 |
(7) |
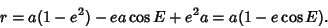 |
(8) |
Differentiating gives
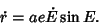 |
(9) |
The eccentric anomaly is a very useful concept in orbital mechanics,  where it is
related to the so-called mean anomaly
where it is
related to the so-called mean anomaly 
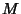 by Kepler's Equation
by Kepler's Equation
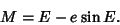 |
(10) |
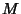 can also be interpreted as the Area of the shaded region in the above figure (Finch).
can also be interpreted as the Area of the shaded region in the above figure (Finch).
See also Eccentricity, Ellipse, Kepler's Equation
References
Danby, J. M. Fundamentals of Celestial Mechanics, 2nd ed., rev. ed. Richmond, VA: Willmann-Bell, 1988.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lpc/lpc.html
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and Focus
and Focus ![]() , and
drawing a Line Perpendicular to the Semimajor Axis and intersecting it at
, and
drawing a Line Perpendicular to the Semimajor Axis and intersecting it at ![]() . The Angle
. The Angle ![]() is
then defined as illustrated above. Then for an Ellipse with Eccentricity
is
then defined as illustrated above. Then for an Ellipse with Eccentricity ![]() ,
,