|
|
|
Let ![]() be the mean anomaly
be the mean anomaly ![]() and
and ![]() the Eccentric Anomaly of a body orbiting on an
Ellipse with Eccentricity
the Eccentric Anomaly of a body orbiting on an
Ellipse with Eccentricity ![]() , then
, then
| (1) |
Writing a ![]() as a Power Series in
as a Power Series in ![]() gives
gives
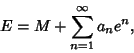 |
(2) |
![\begin{displaymath}
a_n={1\over 2^{n-1}n!} \sum_{k=0}^{\left\lfloor{n/2}\right\rfloor } (-1)^k{n\choose k}(n-2k)^{n-1}\sin[(n-2k)M]
\end{displaymath}](k_373.gif) |
(3) |
| (4) |
| (5) |
There is also a series solution in Bessel Functions of the First Kind,
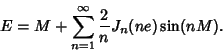 |
(6) |
| (7) |
The equation can also be solved by letting ![]() be the Angle between the planet's motion and the
direction Perpendicular to the Radius Vector. Then
be the Angle between the planet's motion and the
direction Perpendicular to the Radius Vector. Then
| (8) |
| (9) |
| (10) |
| (11) |
Iterative methods such as the simple
| (12) |
| (13) |
In solving Kepler's equation, Stieltjes required the solution to
| (14) |
See also Eccentric Anomaly
References
Danby, J. M. Fundamentals of Celestial Mechanics, 2nd ed., rev. ed. Richmond, VA: Willmann-Bell, 1988.
Dörrie, H. ``The Kepler Equation.'' §81 in
100 Great Problems of Elementary Mathematics: Their History and Solutions.
New York: Dover, pp. 330-334, 1965.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lpc/lpc.html
Goldstein, H. Classical Mechanics, 2nd ed. Reading, MA: Addison-Wesley, pp. 101-102
and 123-124, 1980.
Goursat, E. A Course in Mathematical Analysis, Vol. 2. New York: Dover, p. 120, 1959.
Henrici, P. Applied and Computational Complex Analysis, Vol. 1: Power Series-Integration-Conformal Mapping-Location of Zeros.
New York: Wiley, 1974.
Ioakimids, N. I. and Papadakis, K. E. ``A New Simple Method for the Analytical Solution of Kepler's Equation.''
Celest. Mech. 35, 305-316, 1985.
Ioakimids, N. I. and Papadakis, K. E. ``A New Class of Quite Elementary Closed-Form Integrals Formulae for Roots
of Nonlinear Systems.'' Appl. Math. Comput. 29, 185-196, 1989.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 36, 1983.
Marion, J. B. and Thornton, S. T. ``Kepler's Equations.'' §7.8 in
Classical Dynamics of Particles & Systems, 3rd ed.
San Diego, CA: Harcourt Brace Jovanovich, pp. 261-266, 1988.
Moulton, F. R. An Introduction to Celestial Mechanics, 2nd rev. ed. New York: Dover, pp. 159-169, 1970.
Siewert, C. E. and Burniston, E. E. ``An Exact Analytical Solution of Kepler's Equation.'' Celest. Mech. 6, 294-304, 1972.
Wintner, A. The Analytic Foundations of Celestial Mechanics. Princeton, NJ: Princeton University Press, 1941.
|
|
|
© 1996-9 Eric W. Weisstein