In Cylindrical Coordinates, the Scale Factors are  ,
, 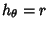 ,
,  and the separation functions are
and the separation functions are 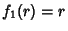 ,
,  ,
, 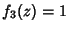 , so the Stäckel Determinant is 1. Attempt Separation of Variables by writing
, so the Stäckel Determinant is 1. Attempt Separation of Variables by writing
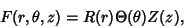 |
(1) |
then the Helmholtz Differential Equation becomes
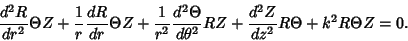 |
(2) |
Now divide by 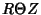 ,
,
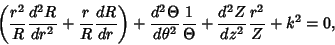 |
(3) |
so the equation has been separated. Since the solution must be periodic in  from the definition of the circular
cylindrical coordinate system, the solution to the second part of (3) must have a Negative separation constant
from the definition of the circular
cylindrical coordinate system, the solution to the second part of (3) must have a Negative separation constant
 |
(4) |
which has a solution
 |
(5) |
Plugging (5) back into (3) gives
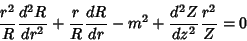 |
(6) |
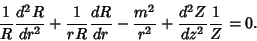 |
(7) |
The solution to the second part of (7) must not be sinusoidal at 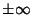 for a physical solution, so the
differential equation has a Positive separation constant
for a physical solution, so the
differential equation has a Positive separation constant
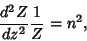 |
(8) |
and the solution is
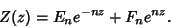 |
(9) |
Plugging (9) back into (7) and multiplying through by  yields
yields
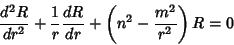 |
(10) |
![\begin{displaymath}
{1\over n^2}{d^2R\over dr^2}+ {1\over (nr)}{1\over n}{dR\over dr} + \left[{1 - {m^2\over (nr)^2}}\right]R = 0
\end{displaymath}](h_950.gif) |
(11) |
![\begin{displaymath}
{d^2R\over d(nr)^2}+ {1\over (nr)}{dR\over d(nr)}+\left[{1-{m^2\over(nr)^2}}\right]R = 0.
\end{displaymath}](h_951.gif) |
(12) |
This is the Bessel Differential Equation, which has a solution
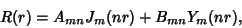 |
(13) |
where 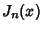 and
and 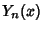 are Bessel Functions of the First and
Second Kinds, respectively. The general solution is therefore
are Bessel Functions of the First and
Second Kinds, respectively. The general solution is therefore
![$F(r, \theta, z) =\sum_{m=0}^\infty\sum_{n=0}^\infty [A_{mn}J_m(nr)+B_{mn}Y_m(nr)]$](h_955.gif)
|
|
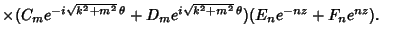
|
(14) |
Actually, the Helmholtz Differential Equation is separable for general  of the form
of the form
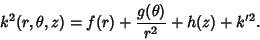 |
(15) |
See also Cylindrical Coordinates, Helmholtz Differential Equation
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, pp. 514 and 656-657, 1953.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() ,
, ![]() ,
, ![]() and the separation functions are
and the separation functions are ![]() ,
, ![]() ,
, ![]() , so the Stäckel Determinant is 1. Attempt Separation of Variables by writing
, so the Stäckel Determinant is 1. Attempt Separation of Variables by writing
![]() for a physical solution, so the
differential equation has a Positive separation constant
for a physical solution, so the
differential equation has a Positive separation constant
![]() of the form
of the form