Using the Notation of Byerly (1959, pp. 252-253), Laplace's Equation can be reduced to
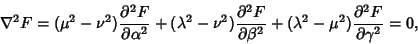 |
(1) |
where
In terms of 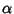 ,
,  , and
, and  ,
,
Equation (1) is not separable using a function of the form
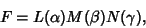 |
(8) |
but it is if we let
These give
and all others terms vanish. Therefore (1) can be broken up into the equations
For future convenience, now write
then
Now replace 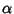 ,
,  , and
, and  to obtain
to obtain
Each of these is a Lamé's Differential Equation, whose solution is called an Ellipsoidal Harmonic.
Writing
gives the solution to (1) as a product of Ellipsoidal Harmonics 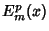 .
.
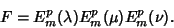 |
(28) |
References
Arfken, G. ``Confocal Ellipsoidal Coordinates
 .'' §2.15 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 117-118, 1970.
.'' §2.15 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 117-118, 1970.
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics,
with Applications to Problems in Mathematical Physics. New York: Dover, pp. 251-258, 1959.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, p. 663, 1953.
© 1996-9 Eric W. Weisstein
1999-05-25
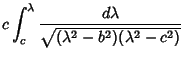
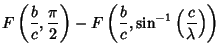
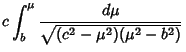
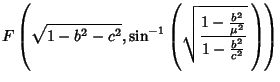
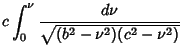
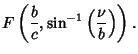
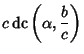
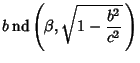
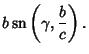
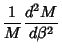
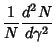
![$\displaystyle {d^2L\over d\alpha^2}-[m(m+1)\lambda^2-(b^2+c^2)p]L$](h_991.gif)
![$\displaystyle {d^2M\over d\beta^2}+[m(m+1)\mu^2-(b^2+c^2)p]M$](h_992.gif)
![$\displaystyle {d^2N\over d\gamma^2}-[m(m+1)\nu^2-(b^2+c^2)p]N$](h_993.gif)
![$\displaystyle (\lambda^2-b^2)(\lambda^2-c^2){d^2L\over d\lambda^2}+\lambda(\lambda^2-b^2+\lambda^2-c^2){dL\over d\lambda}-[m(m+1)\lambda^2-(b^2+c^2)p]L$](h_994.gif)
![$\displaystyle (\mu^2-b^2)(\mu^2-c^2){d^2M\over d\mu^2}+\mu(\mu^2-b^2+\mu^2-c^2){dM\over d\mu}-[m(m+1)\mu^2-(b^2+c^2)p]M$](h_995.gif)
![$\displaystyle (\nu^2-b^2)(\nu^2-c^2){d^2N\over d\nu^2}+\nu(\nu^2-b^2+\nu^2-c^2){dN\over d\nu}-[m(m+1)\nu^2-(b^2+c^2)p]N$](h_996.gif)
![]() .'' §2.15 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 117-118, 1970.
.'' §2.15 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 117-118, 1970.