An important result in Valuation Theory which gives information on finding roots of Polynomials.
Hensel's lemma is formally stated as follow. Let 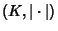 be a complete non-Archimedean valuated field, and let
be a complete non-Archimedean valuated field, and let  be
the corresponding Valuation Ring. Let
be
the corresponding Valuation Ring. Let  be a Polynomial whose Coefficients are in
be a Polynomial whose Coefficients are in
 and suppose
and suppose 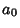 satisfies
satisfies
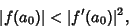 |
(1) |
where 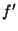 is the (formal) Derivative of
is the (formal) Derivative of  . Then there exists a unique element
. Then there exists a unique element 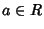 such that
such that 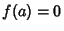 and
and
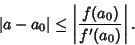 |
(2) |
Less formally, if  is a Polynomial with ``Integer'' Coefficients and
is a Polynomial with ``Integer'' Coefficients and 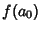 is
``small'' compared to
is
``small'' compared to 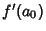 , then the equation
, then the equation  has a solution ``near''
has a solution ``near'' 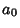 . In addition, there are no other
solutions near
. In addition, there are no other
solutions near 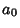 , although there may be other solutions. The proof of the Lemma is based around the Newton-Raphson
method and relies on the non-Archimedean nature of the valuation.
, although there may be other solutions. The proof of the Lemma is based around the Newton-Raphson
method and relies on the non-Archimedean nature of the valuation.
Consider the following example in which Hensel's lemma is used to determine that the equation 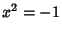 is solvable in
the 5-adic numbers
is solvable in
the 5-adic numbers 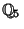 (and so we can embed the Gaussian Integers inside
(and so we can embed the Gaussian Integers inside 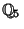 in a nice way). Let
in a nice way). Let  be the 5-adic numbers
be the 5-adic numbers 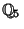 , let
, let 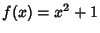 , and let
, and let 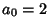 . Then we have
. Then we have 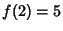 and
and 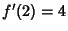 , so
, so
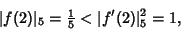 |
(3) |
and the condition is satisfied. Hensel's lemma then tells us that there is a
5-adic number  such that
such that 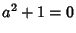 and
and
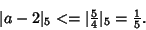 |
(4) |
Similarly, there is a 5-adic number  such that
such that 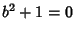 and
and
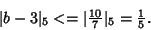 |
(5) |
Therefore, we have found both the square roots of  in
in 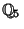 . It is possible to find the roots of any
Polynomial using this technique.
. It is possible to find the roots of any
Polynomial using this technique.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() be a complete non-Archimedean valuated field, and let
be a complete non-Archimedean valuated field, and let ![]() be
the corresponding Valuation Ring. Let
be
the corresponding Valuation Ring. Let ![]() be a Polynomial whose Coefficients are in
be a Polynomial whose Coefficients are in
![]() and suppose
and suppose ![]() satisfies
satisfies
![]() is solvable in
the 5-adic numbers
is solvable in
the 5-adic numbers ![]() (and so we can embed the Gaussian Integers inside
(and so we can embed the Gaussian Integers inside ![]() in a nice way). Let
in a nice way). Let ![]() be the 5-adic numbers
be the 5-adic numbers ![]() , let
, let ![]() , and let
, and let ![]() . Then we have
. Then we have ![]() and
and ![]() , so
, so