|
|
|
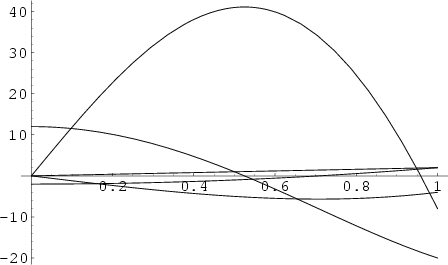
A set of Orthogonal Polynomials. The Hermite polynomials ![]() are illustrated above for
are illustrated above for ![]() and
and ![]() , 2,
..., 5.
, 2,
..., 5.
The Generating Function for Hermite polynomials is
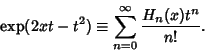 |
(1) |
![$\displaystyle \left[{\left({\partial\over \partial t}\right)^n\mathop{\rm exp}\nolimits (2xt-t^2)}\right]_{t=0}$](h_1417.gif) |
|||
![$\displaystyle \left[{e^{x^2}\left({\partial\over \partial t}\right)^ne^{-(x-t)^2}}\right]_{t=0}.$](h_1418.gif) |
(2) |
![$\displaystyle (-1)^ne^{x^2}\left[{\left({\partial\over \partial x}\right)^ne^{-(x-t)^2}}\right]_{t=0}$](h_1420.gif) |
|||
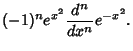 |
(3) |
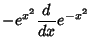 |
(4) | ||
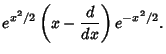 |
(5) |
![$\displaystyle -e^{x^2} {d\over dx} [fe^{-x^2}] = 2xf - {df\over dx}$](h_1427.gif) |
(6) | ||
![$\displaystyle e^{x^2/2}\left({x - {d\over dx}}\right)[fe^{-x^2/2}]$](h_1429.gif) |
|||
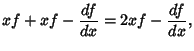 |
(7) |
| (8) |
| (9) |
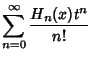 |
(10) | ||
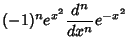 |
(11) | ||
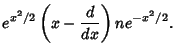 |
(12) |
| (13) |
| (14) |
| (15) |
| (16) |
These obey the orthogonality conditions
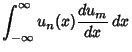 |
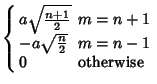 |
(17) | |
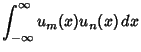 |
(18) | ||
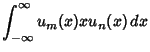 |
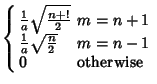 |
(19) | |
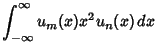 |
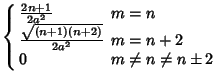 |
||
| (20) | |||
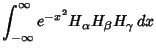 |
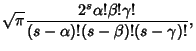 |
||
| (21) |
They also satisfy the Recurrence Relations
| (22) |
| (23) |
The Discriminant is
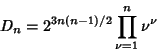 |
(24) |
An interesting identity is
![\begin{displaymath}
\sum_{\nu=0}^n{n\choose\nu}H_\nu(x)H_{n-\nu}(y)=2^{n/2}H_n[2^{-1/2}(x+y)].
\end{displaymath}](h_1459.gif) |
(25) |
The first few Polynomials are
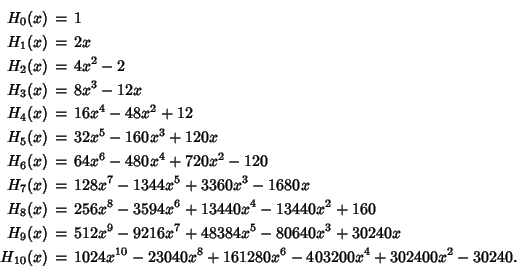
A class of generalized Hermite Polynomials ![]() satisfying
satisfying
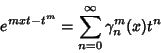 |
(26) |
| (27) |
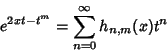 |
(28) |
| (29) |
A modified version of the Hermite Polynomial is sometimes defined by
| (30) |
See also Mehler's Hermite Polynomial Formula, Weber Functions
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 771-802, 1972.
Arfken, G. ``Hermite Functions.'' §13.1 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 712-721, 1985.
Chebyshev, P. L. ``Sur le développement des fonctions à une seule variable.'' Bull. ph.-math.,
Acad. Imp. Sc. St. Pétersbourg 1, 193-200, 1859.
Chebyshev, P. L. Oeuvres, Vol. 1. New York: Chelsea, pp. 49-508, 1987.
Djordjevic, G. ``On Some Properties of Generalized Hermite Polynomials.'' Fib. Quart. 34, 2-6, 1996.
Hermite, C. ``Sur un nouveau développement en série de fonctions.'' Compt. Rend. Acad. Sci. Paris 58,
93-100 and 266-273, 1864. Reprinted in Hermite, C. Oeuvres complètes, Vol. 2. Paris, pp. 293-308, 1908.
Hermite, C. Oeuvres complètes, Vol. 3. Paris, p. 432, 1912.
Iyanaga, S. and Kawada, Y. (Eds.). ``Hermite Polynomials.'' Appendix A, Table 20.IV in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1479-1480, 1980.
Sansone, G. ``Expansions in Laguerre and Hermite Series.'' Ch. 4 in Orthogonal Functions, rev. English ed.
New York: Dover, pp. 295-385, 1991.
Spanier, J. and Oldham, K. B. ``The Hermite Polynomials
Subramanyan, P. R. ``Springs of the Hermite Polynomials.'' Fib. Quart. 28, 156-161, 1990.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.
![]() .''
Ch. 24 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 217-223, 1987.
.''
Ch. 24 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 217-223, 1987.
|
|
|
© 1996-9 Eric W. Weisstein