|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
A Product involving an Infinite number of terms. Such products can converge. In fact, for Positive
![]() , the Product
, the Product
![]() converges to a Nonzero number Iff
converges to a Nonzero number Iff
![]() converges.
converges.
Infinite products can be used to define the Cosine
![\begin{displaymath}
\cos x=\prod_{n=1}^\infty \left[{1-{4x^2\over\pi^2(2n-1)^2}}\right],
\end{displaymath}](i_441.gif) |
(1) |
![\begin{displaymath}
\Gamma(z)=\left[{ze^{\gamma z}\prod_{r=1}^\infty \left({1 + {z\over r}}\right)e^{-z/r}}\right]^{-1},
\end{displaymath}](i_442.gif) |
(2) |
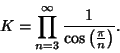 |
(3) |
![$\displaystyle {2\over \prod_{i=n}^\infty \left[{1+{\sin({\textstyle{1\over 2}}\pi p_n)\over p_n}}\right]}$](i_446.gif) |
(4) | ||
![$\displaystyle {2\over \prod_{i=n}^\infty \left[{1+{(-1)^{(p_n-1)/2}\over p_n}}\right]}$](i_447.gif) |
(5) |
The product
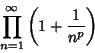 |
(6) |
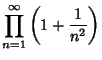 |
(7) | ||
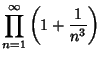 |
(8) | ||
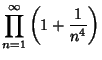 |
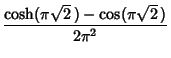 |
(9) | |
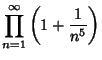 |
(10) |
![\begin{displaymath}[\infty!]_d=\prod_{n=3}^\infty \left({1-{2^d\over n^d}}\right)
\end{displaymath}](i_458.gif) |
(11) |
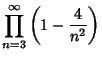 |
(12) | ||
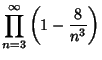 |
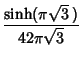 |
(13) | |
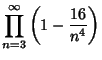 |
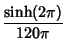 |
(14) | |
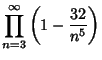 |
(15) |
See also Cosine, Dirichlet Eta Function, Euler Identity, Gamma Function, Iterated Exponential Constants, Polygon Circumscribing Constant, Polygon Inscribing Constant, Q-Function, Sine
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 75, 1972.
Arfken, G. ``Infinite Products.'' §5.11 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 346-351, 1985.
Blatner, D. The Joy of Pi. New York: Walker, p. 119, 1997.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/infprd/infprd.html
Hansen, E. R. A Table of Series and Products. Englewood Cliffs, NJ: Prentice-Hall, 1975.
Whittaker, E. T. and Watson, G. N. §7.5 and 7.6 in A Course in Modern Analysis, 4th ed.
Cambridge, England: Cambridge University Press, 1990.
|
|
|
© 1996-9 Eric W. Weisstein