Laguerre-Gauss Quadrature

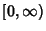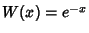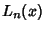Also called Gauss-Laguerre Quadrature or Laguerre Quadrature. A Gaussian Quadrature over the interval $[0, \infty)$ with Weighting Function $W(x)=e^{-x}$. The Abscissas for quadrature order $n$ are given by the Roots of the Laguerre Polynomials $L_n(x)$. The weights are

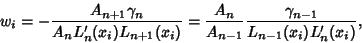$$w_i=-{A_{n+1}\gamma_n\over A_nL_n'(x_i)L_{n+1}(x_i)} ={A_n\over A_{n-1}}{\gamma_{n-1}\over L_{n-1}(x_i)L_n'(x_i)},$$ (1)

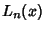where $A_n$ is the Coefficient of $x^n$ in $L_n(x)$. For Laguerre Polynomials,

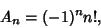$$A_n=(-1)^n n!,$$ (2)

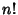where $n!$ is a Factorial, so

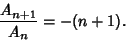$${A_{n+1}\over A_n}=-(n+1).$$ (3)

Additionally,

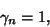$$\gamma_n=1,$$ (4)

so

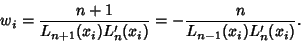$$w_i={n+1\over L_{n+1}(x_i)L_n'(x_i)}=-{n\over L_{n-1}(x_i)L_n'(x_i)}.$$ (5)

(Note that the normalization used here is different than that in Hildebrand 1956.) Using the recurrence relation

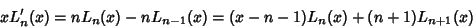$$xL_n'(x)=nL_n(x)-nL_{n-1}(x) =(x-n-1)L_n(x)+(n+1)L_{n+1}(x)$$ (6)

which implies

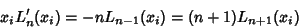$$x_iL_n'(x_i)=-nL_{n-1}(x_i)=(n+1)L_{n+1}(x_i)$$ (7)

gives

$$w_i={1\over x_i[L_n'(x_i)]^2}={x_i\over (n+1)^2[L_{n+1}(x_i)]^2}.$$ (8)

The error term is

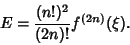$$E={(n!)^2\over(2n)!}f^{(2n)}(\xi).$$ (9)

Beyer (1987) gives a table of Abscissas and weights up to 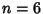$n=6$.

$n$	$x_i$	$w_i$
2	0.585786	0.853553
	3.41421	0.146447
3	0.415775	0.711093
	2.29428	0.278518
	6.28995	0.0103893
4	0.322548	0.603154
	1.74576	0.357419
	4.53662	0.0388879
	9.39507	0.000539295
5	0.26356	0.521756
	1.4134	0.398667
	3.59643	0.0759424
	7.08581	0.00361176
	12.6408	0.00002337

The Abscissas and weights can be computed analytically for small $n$.

$n$	$x_i$	$w_i$
2	$2-\sqrt{2}$	${\textstyle{1\over 4}}(2+\sqrt{2})$
	$2+\sqrt{2}$	${\textstyle{1\over 4}}(2-\sqrt{2})$

For the associated Laguerre polynomial 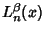$L_n^\beta(x)$ with Weighting Function $w(x)=x^\beta e^{-x}$,

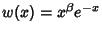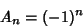$$A_n=(-1)^n$$ (10)

and

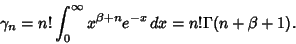$$\gamma_n=n!\int_0^\infty x^{\beta+n}e^{-x}\,dx=n!\Gamma(n+\beta+1).$$ (11)

The weights are

$$w_i={n!\Gamma(n+\beta+1)\over x_i[{L_m^\beta}'(x_i)]^2}={n!\Gamma(n+\beta+1)x_i\over [L_{n+1}^\beta(x_i)]^2},$$ (12)

where $\Gamma(z)$ is the Gamma Function, and the error term is

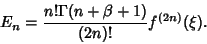$$E_n={n!\Gamma(n+\beta+1)\over(2n)!}f^{(2n)}(\xi).$$ (13)

References

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 463, 1987.

Chandrasekhar, S. Radiative Transfer. New York: Dover, pp. 64-65, 1960.

Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 325-327, 1956.