Laplacian

The Laplacian operator for a Scalar function 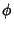$\phi$ is defined by

$$\nabla^2 \phi = {1\over h_1h_2h_3}\left[{{\partial \over \pa... ...h_2\over h_3}{\partial \over \partial u_3}}\right)}\right]\phi$$ (1)

in Vector notation, where the $h_i$ are the Scale Factors of the coordinate system. In Tensor notation, the Laplacian is written

$$\nabla^2\phi = (g^{\lambda\kappa}\phi _{;\lambda})_{;\kappa}= g^{\lambda\kappa}{... ...\lambda\partial x^\kappa}-\Gamma^\lambda {\partial\phi\over\partial x^\lambda }$$

$$= {1\over\sqrt{g}}{\partial\over\partial x^j}\left({\sqrt{g}g^{ij}{\partial\phi\over\partial x^i}}\right),$$ (2)

where $g_{;\kappa}$ is a Covariant Derivative and

$$\Gamma^\lambda \equiv {\textstyle{1\over 2}}g^{\mu\nu}g^{\la... ...l x^\mu}-{\partial g_{\mu\nu}\over \partial x^\kappa}}\right).$$ (3)

The finite difference form is

$\nabla^2\psi(x,y,z) = {1\over h^2}[\psi(x+h,y,z)+\psi(x-h,y,z)$
$+\psi(x,y+h,z)+\psi(x,y-h,z)+\psi(x,y,z+h)$
$+\psi(x,y,z-h)-6\psi(x,y,z)].\quad$	(4)

For a pure radial function $g(r)$,

$$\nabla^2 g(r) \equiv \nabla \cdot [\nabla g(r)]$$

$$= \nabla \cdot \left[{{\partial g(r)\over \partial r}\hat {\bf r} +... ...r\sin \theta}{\partial g(r)\over \partial \phi}\hat {\boldsymbol{\phi}}}\right]$$

$$= \nabla \cdot \left({\hat {\bf r}{dg\over dr}}\right).$$ (5)

Using the Vector Derivative identity

$$\nabla\cdot (f{\bf A}) = f(\nabla\cdot{\bf A})+(\nabla f)\cdot(\bf A),$$ (6)

so

$$\nabla^2 g(r) \equiv \nabla \cdot [\nabla g(r)] = {dg\over dr}\nabla \cdot \hat {\bf r}+ \nabla \left({dg\over dr}\right)\cdot \hat {\bf r}$$

$$= {2\over r}{dg\over dr}+ {d^2g\over dr^2}.$$ (7)

Therefore, for a radial Power law,

$$\nabla^2r^n = {2\over r}nr^{n-1}+n(n-1)r^{n-2}= [2n+n(n-1)]r^{n-2}$$

$$= n(n+1)r^{n-2}.$$ (8)

A Vector Laplacian can also be defined for a Vector A by

$$\nabla^2{\bf A}=\nabla(\nabla\cdot {\bf A})-\nabla\times(\nabla\times{\bf A})$$ (9)

in vector notation. In tensor notation, A is written $A_\mu$, and the identity becomes

$$\nabla^2 A_\mu = {A_{\mu;\lambda}}^{;\lambda} = (g^{\lambda\kappa}A_{\mu;\lambda })_{;\kappa}$$

$$= {g^\lambda\kappa}_{;\kappa}A_{\mu;\lambda}+g^{\lambda\kappa}A_{\mu;\lambda \kappa}.$$ (10)

Similarly, a Tensor Laplacian can be given by

$$\nabla^2 A_{\alpha \beta}= {A_{\alpha \beta ;\lambda}}^{;\lambda}.$$ (11)

An identity satisfied by the Laplacian is

$$\nabla^2 \vert{\bf x}{\hbox{\sf A}}\vert = {{\vert{\hbox{\sf... ...sf A}}^{\rm T}\vert^2\over \vert{\bf x}{\hbox{\sf A}}\vert^3},$$ (12)

where $\vert{\hbox{\sf A}}\vert _2$ is the Hilbert-Schmidt Norm, ${\bf x}$ is a row Vector, and ${\hbox{\sf A}}^{\rm T}$ is the Matrix Transpose of A.

To compute the Laplacian of the inverse distance function $1/r$, where $r\equiv\vert{\bf r}-{\bf r}'\vert$, and integrate the Laplacian over a volume,

$$\int_V \nabla^2 \left({1\over \vert{\bf r}-{\bf r}'\vert}\right)d^3{\bf r}.$$ (13)

This is equal to

$$\int_V \nabla^2 {1\over r}d^3{\bf r} = \int_V \nabla \cdot\left({\nabla {1\over r}}\right)d^3{\bf r} = \int_S \left({\nabla {1\over r}}\right)\cdot d{\bf a}$$

$$= \int_S {\partial \over \partial r}\left({1\over r}\right)\hat {\bf r}\cdot d{\bf a} = \int_S - {1\over r^2}\hat {\bf r}\cdot d{\bf a}$$

$$= - 4\pi {R^2\over r^2},$$ (14)

where the integration is over a small Sphere of Radius $R$. Now, for $r > 0$ and $R\to 0$, the integral becomes 0. Similarly, for $r = R$ and $R\to 0$, the integral becomes $-4\pi$. Therefore,

$$\nabla^2\left({1\over \vert{\bf r}-{\bf r}'\vert}\right)= -4\pi \delta^3({\bf r}-{\bf r}'),$$ (15)

where $\delta({\bf x})$ is the Delta Function.

See also Antilaplacian