|
|
|
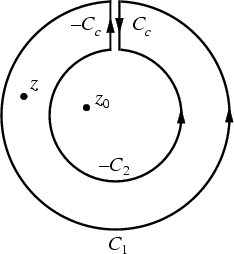
Let there be two circular contours ![]() and
and ![]() , with the radius of
, with the radius of ![]() larger than that of
larger than that of ![]() . Let
. Let ![]() be
interior to
be
interior to ![]() and
and ![]() , and
, and ![]() be between
be between ![]() and
and ![]() . Now create a cut line
. Now create a cut line ![]() between
between ![]() and
and ![]() ,
and integrate around the path
,
and integrate around the path
![]() , so that the plus and minus contributions of
, so that the plus and minus contributions of ![]() cancel one
another, as illustrated above. From the Cauchy Integral Formula,
cancel one
another, as illustrated above. From the Cauchy Integral Formula,
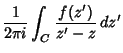 |
|||
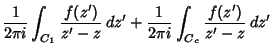 |
|||
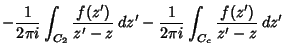 |
|||
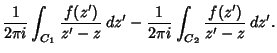 |
(1) |
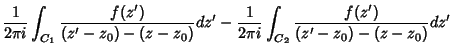 |
|||
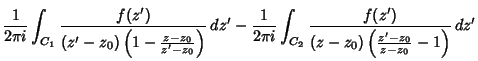 |
|||
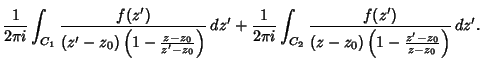 |
(2) |
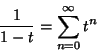 |
(3) |
![$\displaystyle {1\over 2\pi i}\left[{\int_{C_1}{f(z')\over z'-z_0}\sum_{n=0}^\in...
...')\over z-z_0}\sum_{n=0}^\infty \left({z'-z_0\over z-z_0}\right)^n\,dz'}\right]$](l1_907.gif) |
|||
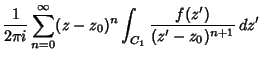 |
|||
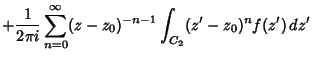 |
|||
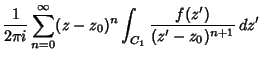 |
|||
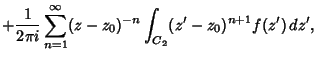 |
(4) |
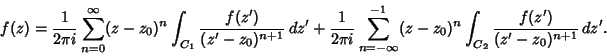 |
(5) |
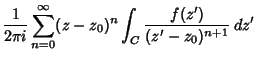 |
|||
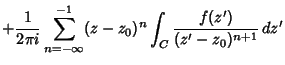 |
|||
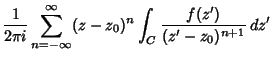 |
|||
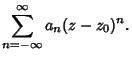 |
(6) |
The only requirement on ![]() is that it encloses
is that it encloses ![]() , so we are free to choose any contour
, so we are free to choose any contour ![]() that does so. The
Residues
that does so. The
Residues ![]() are therefore defined by
are therefore defined by
| (7) |
See also Maclaurin Series, Residue (Complex Analysis), Taylor Series
References
Arfken, G. ``Laurent Expansion.'' §6.5 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 376-384, 1985.
Morse, P. M. and Feshbach, H. ``Derivatives of Analytic Functions, Taylor and Laurent Series.'' §4.3 in
Methods of Theoretical Physics, Part I. New York: McGraw-Hill,
pp. 374-398, 1953.
|
|
|
© 1996-9 Eric W. Weisstein