Given a Random Variable 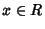 , if there exists an
, if there exists an 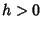 such that
such that
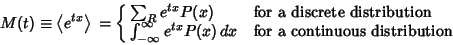 |
(1) |
for 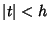 , then
, then
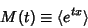 |
(2) |
is the moment-generating function.
where 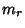 is the
is the  th Moment about zero. The moment-generating function satisfies
th Moment about zero. The moment-generating function satisfies
If 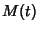 is differentiable at zero, then the
is differentiable at zero, then the 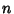 th Moments about the Origin are given by
th Moments about the Origin are given by
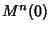
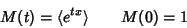 |
(5) |
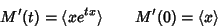 |
(6) |
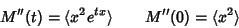 |
(7) |
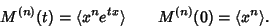 |
(8) |
The Mean and Variance are therefore
It is also true that
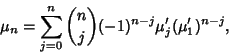 |
(11) |
where 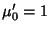 and
and 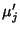 is the
is the 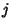 th moment about the origin.
th moment about the origin.
It is sometimes simpler to work with the Logarithm of the moment-generating function, which is also called the
Cumulant-Generating Function, and is defined by
But
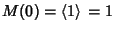 , so
, so
See also Characteristic Function, Cumulant, Cumulant-Generating Function, Moment
References
Kenney, J. F. and Keeping, E. S. ``Moment-Generating and Characteristic Functions,'' ``Some Examples of Moment-Generating Functions,''
and ``Uniqueness Theorem for Characteristic Functions.'' §4.6-4.8 in Mathematics of Statistics, Pt. 2, 2nd ed.
Princeton, NJ: Van Nostrand, pp. 72-77, 1951.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , if there exists an
, if there exists an ![]() such that
such that
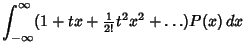
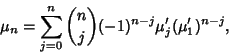
![$\displaystyle {M(t)M''(t)-[M'(t)]^2\over[M(t)]^2}.$](m_1742.gif)