Parabola

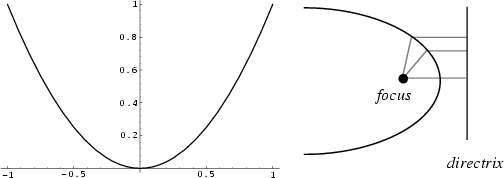
$\begin{figure}\begin{center}\BoxedEPSF{Parabola.epsf scaled 640}\quad\BoxedEPSF{ParabolaDirectrix.epsf scaled 850}\end{center}\end{figure}$

The set of all points in the Plane equidistant from a given Line (the Directrix) and a given point not on the line (the Focus).

The parabola was studied by Menaechmus in an attempt to achieve Cube Duplication. Menaechmus solved the problem by finding the intersection of the two parabolas and . Euclid wrote about the parabola, and it was given its present name by Apollonius. Pascal considered the parabola as a projection of a Circle, and Galileo showed that projectiles falling under uniform gravity follow parabolic paths. Gregory and Newton considered the Catacaustic properties of a parabola which bring parallel rays of light to a focus (MacTutor Archive).

For a parabola opening to the right, the equation in Cartesian Coordinates is

$\begin{displaymath} \sqrt{(x-a)^2+y^2} = x+a \end{displaymath}$

(1)

$\begin{displaymath} (x-a)^2+y^2 = (x+a)^2 \end{displaymath}$

(2)

$\begin{displaymath} x^2-2ax+a^2+y^2 = x^2+2ax+a^2 \end{displaymath}$

(3)

$\begin{displaymath} y^2 = 4ax. \end{displaymath}$

(4)

If the Vertex is at

instead of (0, 0), the equation is

$\begin{displaymath} (y-y_0)^2=4a(x-x_0). \end{displaymath}$

(5)

If the parabola opens upwards,

$\begin{displaymath} x^2 = 4ay \end{displaymath}$

(6)

(which is the form shown in the above figure at left). The quantity

is known as the Latus Rectum. In Polar Coordinates,

$\begin{displaymath} r={2a\over 1-\cos\theta}. \end{displaymath}$

(7)

In Pedal Coordinates with the Pedal Point at the Focus, the equation is

$\begin{displaymath} p^2=ar. \end{displaymath}$

(8)

The parametric equations for the parabola are

$\displaystyle x$	$\textstyle =$	$\displaystyle 2at$	(9)
$\displaystyle y$	$\textstyle =$	$\displaystyle at^2.$	(10)

$\begin{figure}\begin{center}\BoxedEPSF{ParabolaInfo.epsf scaled 720}\end{center}\end{figure}$

The Curvature, Arc Length, and Tangential Angle are

$\displaystyle \kappa(t)$	$\textstyle =$	$\displaystyle {1\over 2(1+t^2)^{3/2}}$	(11)
$\displaystyle s(t)$	$\textstyle =$	$\displaystyle t\sqrt{1+t^2}+\sinh^{-1}t$	(12)
$\displaystyle \phi(t)$	$\textstyle =$	$\displaystyle \tan^{-1}t.$	(13)

The Tangent Vector of the parabola is

$\displaystyle x_T(t)$	$\textstyle =$	$\displaystyle {1\over\sqrt{1+t^2}}$	(14)
$\displaystyle y_T(t)$	$\textstyle =$	$\displaystyle {t\over\sqrt{1+t^2}}.$	(15)

The plots below show the normal and tangent vectors to a parabola.

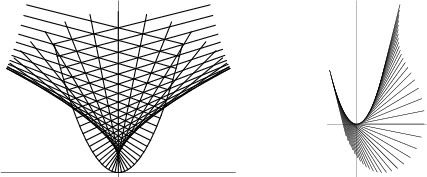
$\begin{figure}\begin{center}\BoxedEPSF{ParabolaNormalTangent.epsf}\end{center}\end{figure}$

References

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 198, 1987.

Casey, J. ``The Parabola.'' Ch. 5 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 173-200, 1893.

Coxeter, H. S. M. ``Conics.'' §8.4 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 115-119, 1969.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 67-72, 1972.

Lee, X. ``Parabola.'' http://www.best.com/~xah/SpecialPlaneCurves_dir/Parabola_dir/parabola.html.

Lockwood, E. H. ``The Parabola.'' Ch. 1 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 2-12, 1967.

MacTutor History of Mathematics Archive. ``Parabola.'' http://www-groups.dcs.st-and.ac.uk/~history/Curves/Parabola.html.

Pappas, T. ``The Parabolic Ceiling of the Capitol.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 22-23, 1989.