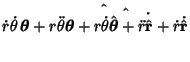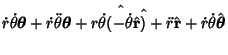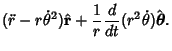The polar coordinates 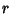 and
and 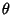 are defined by
are defined by
In terms of  and
and 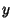 ,
,
The Arc Length of a polar curve given by 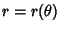 is
is
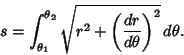 |
(5) |
The Line Element is given by
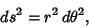 |
(6) |
and the Area element by
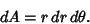 |
(7) |
The Area enclosed by a polar curve 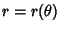 is
is
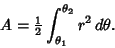 |
(8) |
The Slope of a polar function
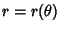 at the point
at the point 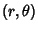 is given by
is given by
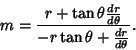 |
(9) |
The Angle between the tangent and radial line at the point 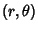 is
is
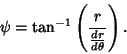 |
(10) |
A polar curve is symmetric about the  -axis if replacing
-axis if replacing 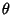 by
by 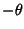 in its equation produces an equivalent
equation, symmetric about the
in its equation produces an equivalent
equation, symmetric about the 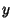 -axis if replacing
-axis if replacing 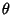 by
by 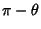 in its equation produces an equivalent
equation, and symmetric about the origin if replacing
in its equation produces an equivalent
equation, and symmetric about the origin if replacing 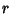 by
by 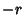 in its equation
produces an equivalent equation.
in its equation
produces an equivalent equation.
In Cartesian coordinates, the Position Vector and its derivatives are
In polar coordinates, the Unit Vectors and their derivatives are
 |
 |
![$\displaystyle \left[\begin{array}{c}r\cos\theta\\ r\sin\theta\end{array}\right]$](p2_1122.gif) |
(15) |
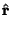 |
 |
![$\displaystyle {{d{\bf r}\over dr}\over \left\vert{d{\bf r}\over dr}\right\vert} = \left[\begin{array}{c}\cos\theta\\ \sin\theta\end{array}\right]$](p2_1123.gif) |
(16) |
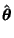 |
 |
![$\displaystyle {{d\boldsymbol{\theta}\over d\theta}\over \left\vert{d\boldsymbol...
...ght\vert} = \left[\begin{array}{c}-\sin \theta\\ \cos \theta\end{array}\right]$](p2_1125.gif) |
(17) |
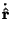 |
 |
![$\displaystyle \left[\begin{array}{c}-\sin\theta\dot\theta\\ \cos\theta\dot\theta\end{array}\right] = \dot\theta\,\hat {\boldsymbol{\theta}}$](p2_1126.gif) |
(18) |
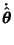 |
 |
![$\displaystyle \left[\begin{array}{c}-\cos\theta\dot\theta\\ -\sin\theta\dot\theta\end{array}\right] = -\dot\theta\hat {\bf r}$](p2_1128.gif) |
(19) |
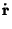 |
 |
![$\displaystyle \left[\begin{array}{c}-r\sin\theta\dot\theta+\cos\theta\dot r\\
...
...nd{array}\right] = r\dot\theta \,\hat\boldsymbol{\theta}+ \dot r \,\hat {\bf r}$](p2_1129.gif) |
|
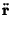 |
 |
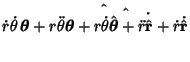 |
|
| |
 |
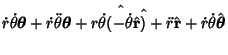 |
|
| |
 |
 |
|
| |
 |
 |
(20) |
See also Cardioid, Circle, Cissoid, Conchoid, Curvilinear Coordinates, Cylindrical
Coordinates, Equiangular Spiral, Lemniscate, Limaçon, Rose
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and
and ![]() are defined by
are defined by
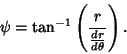
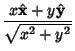
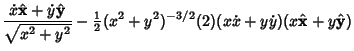
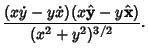
![$\displaystyle \left[\begin{array}{c}r\cos\theta\\ r\sin\theta\end{array}\right]$](p2_1122.gif)
![$\displaystyle {{d{\bf r}\over dr}\over \left\vert{d{\bf r}\over dr}\right\vert} = \left[\begin{array}{c}\cos\theta\\ \sin\theta\end{array}\right]$](p2_1123.gif)
![$\displaystyle {{d\boldsymbol{\theta}\over d\theta}\over \left\vert{d\boldsymbol...
...ght\vert} = \left[\begin{array}{c}-\sin \theta\\ \cos \theta\end{array}\right]$](p2_1125.gif)
![$\displaystyle \left[\begin{array}{c}-\sin\theta\dot\theta\\ \cos\theta\dot\theta\end{array}\right] = \dot\theta\,\hat {\boldsymbol{\theta}}$](p2_1126.gif)
![$\displaystyle \left[\begin{array}{c}-\cos\theta\dot\theta\\ -\sin\theta\dot\theta\end{array}\right] = -\dot\theta\hat {\bf r}$](p2_1128.gif)
![$\displaystyle \left[\begin{array}{c}-r\sin\theta\dot\theta+\cos\theta\dot r\\
...
...nd{array}\right] = r\dot\theta \,\hat\boldsymbol{\theta}+ \dot r \,\hat {\bf r}$](p2_1129.gif)