|
|
|
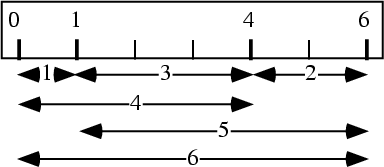
A type of Ruler considered by Guy (1994) which has ![]() distinct marks spaced such that the distances between marks
can be used to measure all the distances 1, 2, 3, 4, ... up to some maximum distance
distinct marks spaced such that the distances between marks
can be used to measure all the distances 1, 2, 3, 4, ... up to some maximum distance ![]() . Such a ruler can be
constructed from a Perfect Difference Set by subtracting one from each element. For example, the Perfect
Difference Set
. Such a ruler can be
constructed from a Perfect Difference Set by subtracting one from each element. For example, the Perfect
Difference Set
![]() gives 0, 1, 4, 6, which can be used to measure
gives 0, 1, 4, 6, which can be used to measure ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() (so we get 6 distances with only four marks).
(so we get 6 distances with only four marks).
See also Perfect Difference Set
References
Guy, R. K. ``Modular Difference Sets and Error Correcting Codes.'' §C10 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 118-121, 1994.