|
|
|
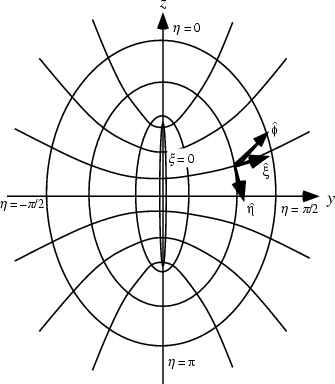
A system of Curvilinear Coordinates in which two sets of coordinate surfaces are obtained by revolving the curves of the
Elliptic Cylindrical Coordinates about the x-Axis, which is relabeled the z-Axis. The third set of coordinates consists of planes passing through this axis.
| (1) | |||
| (2) | |||
| (3) |
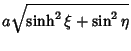 |
(4) | ||
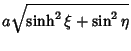 |
(5) | ||
| (6) |
|
|
|
|
|
(7) |
|
|
(8) |
An alternate form useful for ``two-center'' problems is defined by
| (9) | |||
| (10) | |||
| (11) |
| (12) | |||
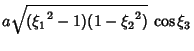 |
(13) | ||
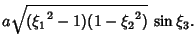 |
(14) |
| (15) | |||
| (16) | |||
| (17) |
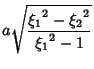 |
(18) | ||
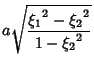 |
(19) | ||
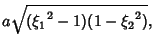 |
(20) |
|
|
|
|
|
(21) |
See also Helmholtz Differential Equation--Prolate Spheroidal Coordinates, Latitude, Longitude, Oblate Spheroidal Coordinates, Spherical Coordinates
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Definition of Prolate Spheroidal Coordinates.'' §21.2 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 752, 1972.
Arfken, G. ``Prolate Spheroidal Coordinates (
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 661, 1953.
![]() ,
, ![]() ,
, ![]() ).'' §2.10 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 103-107, 1970.
).'' §2.10 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 103-107, 1970.
|
|
|
© 1996-9 Eric W. Weisstein