|
|
|
The definition of the (signed) Stirling number of the first kind is a number ![]() such that the number of permutations
of
such that the number of permutations
of ![]() elements which contain exactly
elements which contain exactly ![]() Cycles is
Cycles is
| (1) |
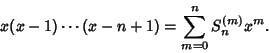 |
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The Nonnegative version simply gives the number of Permutations of ![]() objects having
objects having ![]() Cycles (with cycles in opposite directions counted as distinct) and is obtained by taking the
Absolute Value of the signed version. The nonnegative Stirling number of the first kind is denoted
Cycles (with cycles in opposite directions counted as distinct) and is obtained by taking the
Absolute Value of the signed version. The nonnegative Stirling number of the first kind is denoted
![]() or
or
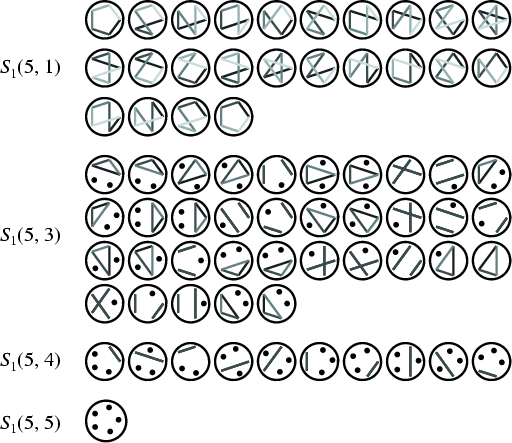
![]() . Diagrams illustrating
. Diagrams illustrating ![]() ,
, ![]() ,
, ![]() , and
, and
![]() (Dickau) are shown below.
(Dickau) are shown below.
The nonnegative Stirling numbers of the first kind satisfy the curious identity
![\begin{displaymath}
\sum_{n=1}^\infty\left[{\,\sum_{k=0}^{n-2} {(e^x-x-1)^{k+1}S_1(n,n-k)\over(k+1)!}}\right]e^{-xn}=\ln(x+1)
\end{displaymath}](s3_942.gif) |
(3) |
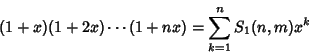 |
(4) |
| (5) |
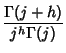 |
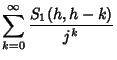 |
||
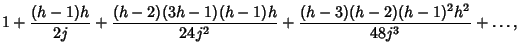 |
(6) |
See also Cycle (Permutation), Harmonic Number, Permutation, Stirling Number of the Second Kind
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Stirling Numbers of the First Kind.'' §24.1.3 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 824, 1972.
Adamchik, V. ``On Stirling Numbers and Euler Sums.'' J. Comput. Appl. Math. 79, 119-130, 1997.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 91-92, 1996.
Dickau, R. M. ``Stirling Numbers of the First Kind.''
http://forum.swarthmore.edu/advanced/robertd/stirling1.html.
Knuth, D. E. ``Two Notes on Notation.'' Amer. Math. Monthly 99, 403-422, 1992.
Sloane, N. J. A. Sequence
A008275
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
|
|
|
© 1996-9 Eric W. Weisstein