The confocal ellipsoidal coordinates (called simply ellipsoidal coordinates by Morse and Feshbach 1953) are given by the
equations
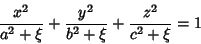 |
(1) |
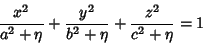 |
(2) |
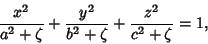 |
(3) |
where
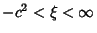 ,
,
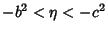 , and
, and
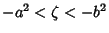 . Surfaces of constant
. Surfaces of constant 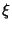 are confocal
Ellipsoids, surfaces of constant
are confocal
Ellipsoids, surfaces of constant 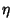 are one-sheeted Hyperboloids, and
surfaces of constant
are one-sheeted Hyperboloids, and
surfaces of constant 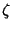 are two-sheeted Hyperboloids. For every
are two-sheeted Hyperboloids. For every 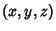 , there is a unique set
of ellipsoidal coordinates. However,
, there is a unique set
of ellipsoidal coordinates. However,
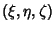 specifies eight points symmetrically located in octants. Solving for
specifies eight points symmetrically located in octants. Solving for
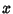 ,
, 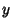 , and
, and 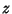 gives
gives
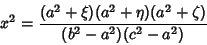 |
(4) |
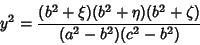 |
(5) |
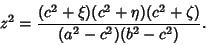 |
(6) |
The Laplacian is
![$\nabla^2\Psi=(\eta-\zeta)f(\xi){\partial\over\partial\xi}\left[{f(\xi){\partial\Psi\over\partial\xi}}\right]$](c2_1066.gif)
|
|
![$ +(\zeta-\xi)f(\eta){\partial\over\partial\eta}\left[{f(\eta){\partial\Psi\over...
...tial\over\partial\zeta}\left[{f(\zeta){\partial\Psi\over\partial\zeta}}\right],$](c2_1067.gif)
|
|
|
|
(7) |
where
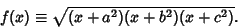 |
(8) |
Another definition is
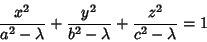 |
(9) |
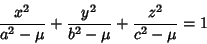 |
(10) |
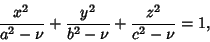 |
(11) |
where
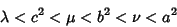 |
(12) |
(Arfken 1970, pp. 117-118). Byerly (1959, p. 251) uses a slightly different definition in which the Greek variables
are replaced by their squares, and 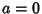 . Equation (9) represents an Ellipsoid, (10) represents a
one-sheeted Hyperboloid, and (11) represents a two-sheeted Hyperboloid. In terms of
Cartesian Coordinates,
. Equation (9) represents an Ellipsoid, (10) represents a
one-sheeted Hyperboloid, and (11) represents a two-sheeted Hyperboloid. In terms of
Cartesian Coordinates,
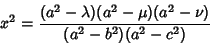 |
(13) |
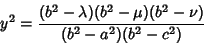 |
(14) |
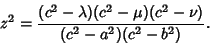 |
(15) |
The Scale Factors are
The Laplacian is
Using the Notation of Byerly (1959, pp. 252-253), this can be reduced to
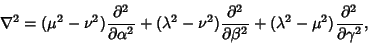 |
(20) |
where
Here, 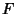 is an Elliptic Integral of the First Kind. In terms of
is an Elliptic Integral of the First Kind. In terms of 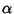 ,
, 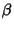 , and
, and 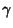 ,
,
where
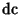 ,
,
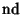 and
and
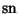 are Jacobi Elliptic Functions. The Helmholtz Differential Equation is separable in
confocal ellipsoidal coordinates.
are Jacobi Elliptic Functions. The Helmholtz Differential Equation is separable in
confocal ellipsoidal coordinates.
See also Helmholtz Differential Equation--Confocal Ellipsoidal Coordinates
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Definition of Elliptical Coordinates.'' §21.1 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 752, 1972.
Arfken, G. ``Confocal Ellipsoidal Coordinates
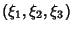 .'' §2.15 in
Mathematical Methods for Physicists, 2nd ed. New York: Academic Press, pp. 117-118, 1970.
.'' §2.15 in
Mathematical Methods for Physicists, 2nd ed. New York: Academic Press, pp. 117-118, 1970.
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical,
Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 663, 1953.
© 1996-9 Eric W. Weisstein
1999-05-26
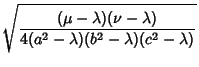
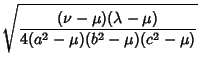
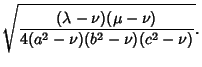
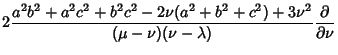
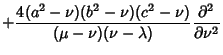
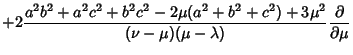
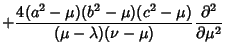
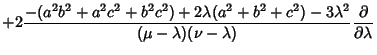
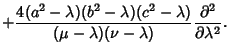
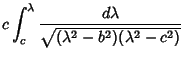
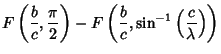
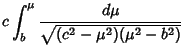
![$\displaystyle F\left[{\sqrt{1-{b^2\over c^2}}, \sin^{-1}\left({\sqrt{1-{b^2\over\mu^2}\over 1-{b^2\over c^2}}\,}\right)}\right]$](c2_1095.gif)
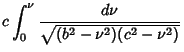
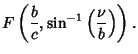
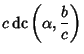
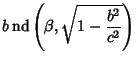
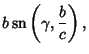
![]() .'' §2.15 in
Mathematical Methods for Physicists, 2nd ed. New York: Academic Press, pp. 117-118, 1970.
.'' §2.15 in
Mathematical Methods for Physicists, 2nd ed. New York: Academic Press, pp. 117-118, 1970.