Hexagon

A six-sided Polygon. In proposition IV.15, Euclid showed how to inscribe a regular hexagon in a Circle. The Inradius $r$, Circumradius $R$, and Area $A$ can be computed directly from the formulas for a general regular Polygon with side length $s$ and $n=6$ sides,

$$r = {\textstyle{1\over 2}}s\cot\left({\pi\over 6}\right)={\textstyle{1\over 2}}\sqrt{3}\,s$$ (1)

$$R = {\textstyle{1\over 2}}s\csc\left({\pi\over 6}\right)=s$$ (2)

$$A = {\textstyle{1\over 4}}ns^2\cot\left({\pi\over 6}\right)={\textstyle{3\over 2}}\sqrt{3}\,s^2.$$ (3)

Therefore, for a regular hexagon,

$${R\over r}=\sec\left({\pi\over 6}\right)={2\over\sqrt{3}},$$ (4)

so

$${A_R\over A_r} = \left({R\over r}\right)^2={4\over 3}.$$ (5)

A Plane Perpendicular to a $C_3$ axis of a Cube, Dodecahedron, or Icosahedron cuts the solid in a regular Hexagonal Cross-Section (Holden 1991, pp. 22-23 and 27). For the Cube, the Plane passes through the Midpoints of opposite sides (Steinhaus 1983, p. 170; Cundy and Rollett 1989, p. 157; Holden 1991, pp. 22-23). Since there are four such axes for the Cube and Octahedron, there are four possible hexagonal cross-sections.

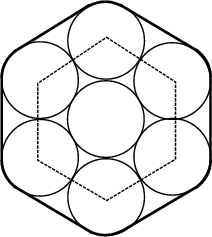
Take seven Circles and close-pack them together in a hexagonal arrangement. The Perimeter obtained by wrapping a band around the Circle then consists of six straight segments of length $d$ (where $d$ is the Diameter) and 6 arcs with total length ${1/6}$ of a Circle. The Perimeter is therefore

$$p=(12+2\pi)r=2(6+\pi)r.$$ (6)

See also Cube, Cyclic Hexagon, Dissection, Dodecahedron, Graham's Biggest Little Hexagon, Hexagon Polyiamond, Hexagram, Magic Hexagon, Octahedron, Pappus's Hexagon Theorem, Pascal's Theorem, Talisman Hexagon

References

Cundy, H. and Rollett, A. ``Hexagonal Section of a Cube.'' §3.15.1 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 157, 1989.

Dixon, R. Mathographics. New York: Dover, p. 16, 1991.

Holden, A. Shapes, Space, and Symmetry. New York: Dover, 1991.

Pappas, T. ``Hexagons in Nature.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 74-75, 1989.

Steinhaus, H. Mathematical Snapshots, 3rd American ed. New York: Oxford University Press, 1983.