A second-order Ordinary Differential Equation arising in the study of stellar interiors. It is given by
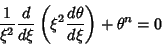 |
(1) |
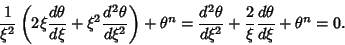 |
(2) |
It has the Boundary Conditions
Solutions  for
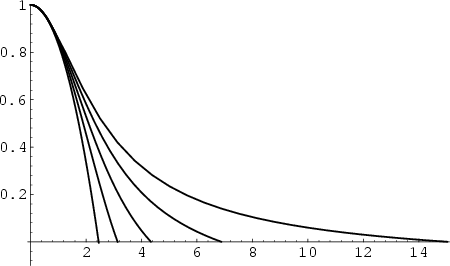
for  , 1, 2, 3, and 4 are shown above. The cases
, 1, 2, 3, and 4 are shown above. The cases 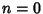 , 1, and 5 can be solved analytically
(Chandrasekhar 1967, p. 91); the others must be obtained numerically.
, 1, and 5 can be solved analytically
(Chandrasekhar 1967, p. 91); the others must be obtained numerically.
For 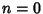 (
(
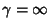 ), the Lane-Emden Differential Equation is
), the Lane-Emden Differential Equation is
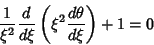 |
(5) |
(Chandrasekhar 1967, pp. 91-92). Directly solving gives
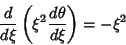 |
(6) |
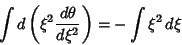 |
(7) |
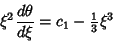 |
(8) |
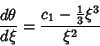 |
(9) |
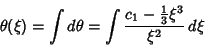 |
(10) |
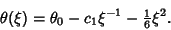 |
(11) |
The Boundary Condition 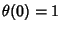 then gives
then gives 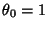 and
and 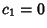 , so
, so
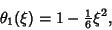 |
(12) |
and 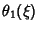 is Parabolic.
is Parabolic.
For  (
(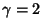 ), the differential equation becomes
), the differential equation becomes
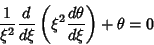 |
(13) |
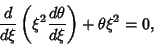 |
(14) |
which is the Spherical Bessel Differential Equation
![\begin{displaymath}
{d\over dr}\left({r^2{dR\over dr}}\right)+[k^2r^2-n(n+1)]R=0
\end{displaymath}](l1_567.gif) |
(15) |
with 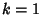 and
and 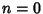 , so the solution is
, so the solution is
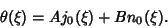 |
(16) |
Applying the Boundary Condition 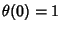 gives
gives
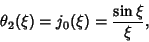 |
(17) |
where 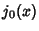 is a Spherical Bessel Function of the First Kind (Chandrasekhar 1967, pp. 92).
is a Spherical Bessel Function of the First Kind (Chandrasekhar 1967, pp. 92).
For 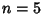 , make Emden's transformation
, make Emden's transformation
which reduces the Lane-Emden equation to
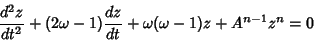 |
(20) |
(Chandrasekhar 1967, p. 90). After further manipulation (not reproduced here), the equation becomes
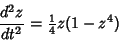 |
(21) |
and then, finally,
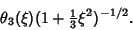 |
(22) |
References
Chandrasekhar, S. An Introduction to the Study of Stellar Structure. New York: Dover, pp. 84-182, 1967.
© 1996-9 Eric W. Weisstein
1999-05-26
![$\displaystyle \left[{d\theta\over d\xi}\right]_{\xi=0}$](l1_548.gif)
![]() (
(
![]() ), the Lane-Emden Differential Equation is
), the Lane-Emden Differential Equation is
![]() (
(![]() ), the differential equation becomes
), the differential equation becomes
![]() , make Emden's transformation
, make Emden's transformation